Problème de mathématiques viral – Calculatrice, livres, ordinateurs portables
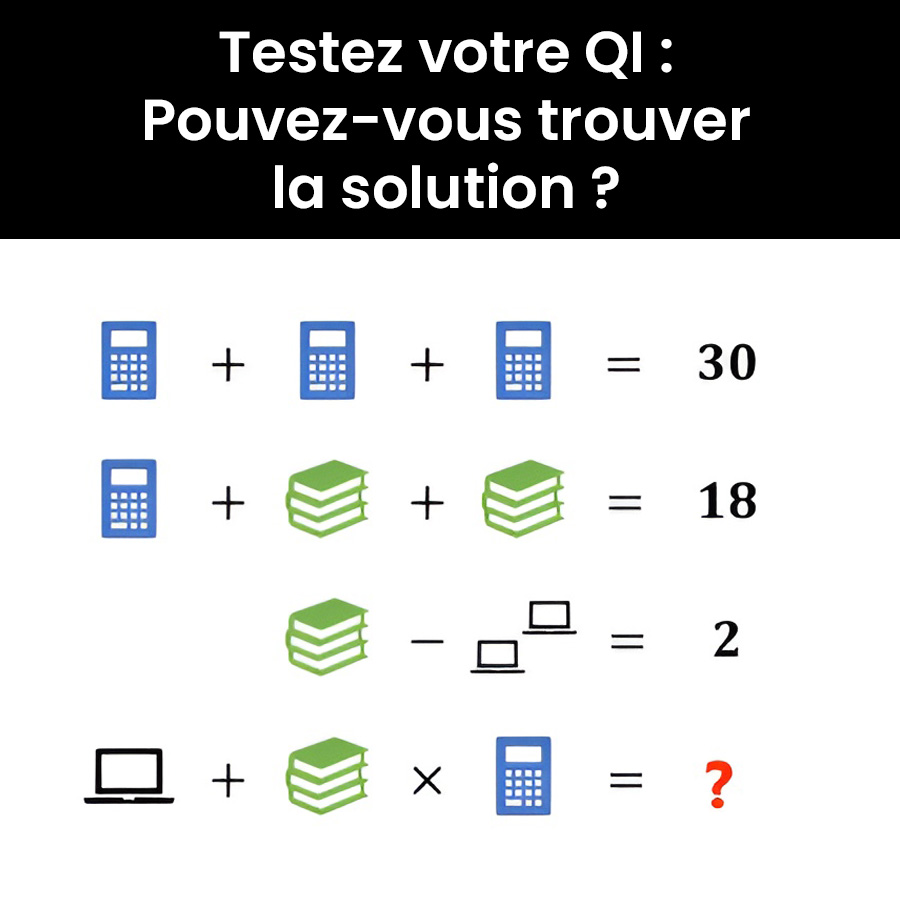
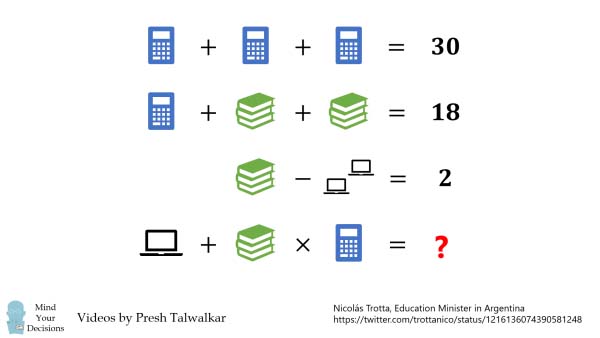
Tout commence par un simple tweet du ministre de l'Éducation argentin, Nicolás Trotta, partageant un problème mathématique. Ce casse-tête, devenu rapidement viral, a divisé les internautes entre plusieurs solutions possibles. Mais pourquoi un problème apparemment simple suscite-t-il autant de débats ?
Le problème
Imaginez une équation où des objets du quotidien comme calculatrices, livres et ordinateurs portables remplacent les nombres. Votre mission ? Trouver la valeur de chaque objet tout en respectant l’équilibre de l’équation. Facile, non ? Pas si sûr !
Ces énigmes visuelles nécessitent une attention particulière, car chaque détail compte :
- Les symboles se ressemblent, mais ne sont pas identiques. Par exemple, un livre peut avoir un nombre de pages différent, ou une calculatrice afficher un écran distinct.
- Les opérations sont classiques, mais la solution réside dans votre capacité d’observation minutieuse.
Résolution du problème
Commençons par définir les variables :
- CC représente une calculatrice,
- BB un ensemble de livres,
- LL une paire d’ordinateurs portables,
- xx un seul ordinateur portable.
Les équations fournies sont les suivantes :
- C+C+C=30C+C+C=30
- C+B+B=18C+B+B=18
- B−L=2B−L=2
- x+B×C=?x+B×C=?
Étape 1 : Résolvons pour CC à partir de la première équation.
C+C+C=30C+C+C=30
3C=303C=30
C=10C=10
Étape 2 : Résolvons pour BB à partir de la deuxième équation.
C+B+B=18C+B+B=18
10+2B=1810+2B=18
2B=82B=8
B=4B=4
Étape 3 : Résolvons pour LL à partir de la troisième équation.
B−L=2B−L=2
4−L=24−L=2
L=2L=2
Étape 4 : Résolvons pour xx.
Sachant que L=2L=2 correspond à une paire d’ordinateurs portables, il est logique d’interpréter cela comme :
2=L=x+x2=L=x+x
x=1x=1
Nous pouvons alors évaluer l’expression suivante :
x+B×Cx+B×C
=1+4×10=1+4×10
=1+40=1+40
=41=41
C’était la solution officielle !
Pourquoi tant de confusion ?
Ce genre de problème ne teste pas seulement vos compétences mathématiques, mais également votre capacité à repérer les différences subtiles et à interpréter correctement l’équation. Cela explique pourquoi tant d’internautes s’acharnent : la solution semble simple, mais le diable est dans les détails.
Une double solution ?

Pour certains, la résolution repose sur une approche classique : identifier chaque valeur et résoudre pas à pas. Mais d’autres estiment qu’une interprétation différente des règles peut aboutir à une solution alternative. Cela démontre que, même en mathématiques, une question peut ouvrir la porte à des discussions inattendues !
Un défi pour les passionnés
Si vous êtes prêt à tester vos compétences, plongez-vous dans ce problème. Et souvenez-vous : parfois, l’essentiel réside moins dans les mathématiques que dans l’observation. Alors, prenez votre temps, amusez-vous et partagez votre réponse !








